探秘斐波拉契数列!

　　介绍

　　 斐波那契数列(Fibonacci sequence)，又称黄金分割数列，因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：*F*(0)=0，*F*(1)=1, *F*(n)=*F*(n - 1)+*F*(n - 2)(*n* ≥ 2，*n* ∈ N*)在现代物理、晶体结构、化学等领域，斐波纳契数列都有直接的应用，为此，美国数学会从 1963 年起出版了以《斐波纳契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。

　　java中如何编码实现斐波那契数列

　　方案1：递归

　　 根据斐波那契数列的数学表示方式：*F*(1)=1，*F*(2)=1, *F*(n)=*F*(n - 1)+*F*(n - 2)(*n* ≥ 2，*n* ∈ N*)

　　 很容易就可以得出：

public int fib(int n) {
    if(n <= 2) return 1;
    return fib(n - 1) + fib(n - 2);
}

　　问题：使用以上代码完成斐波那契数列，时间复杂度是0(n^2),空间复杂度是0(n);

　　 我们以fib(6)为例： 时间复杂度很明显是0(n^2)

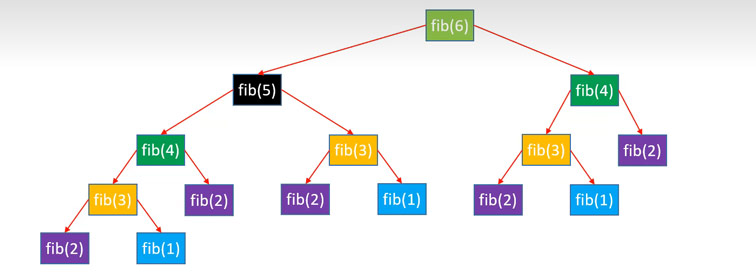
　　空间复杂度是0(n)

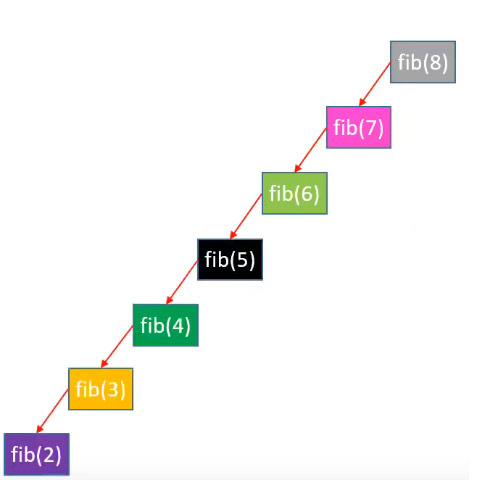
　　方案2： 基于数组进行优化

　　 方案1中很多的代码，存在重复调用.可以考虑使用一个数组存放，之前调用得到的结果;

  public int fib(int n) {
        if(n <= 2) return 1;
        int[] array = new int[n + 1]; //定义数组，存放已经得到结果的数据
        array[1] = array[2] = 1;
        return fib(n,array);
    }

    public int fib(int n,int[] array) {
        if(array[n] == 0) { //判断数组中是否有元素，如果有，直接返回，没有，递归。
            array[n] = fib(n -1 ,array) + fib(n - 2,array);
        }
        return array[n];
    }

　　问题：使用以上代码完成斐波那契数列，时间复杂度是0(n),空间复杂度是0(n);

　　 空间复杂度：额外定义了一个数组;空间复杂度依然是0(n)。

　　 时间复杂度：由于没有了重复的调用，时间复杂度是0(n)。

　　方案3： 将递归转化为非递归优化

　　 定义一个数组存放，存放斐波拉契数列每一项数据;免去递归调用;

  public int fib(int n) {
        if(n <= 2) return 1;
        int[] array = new int[n + 1];
        array[1] = array[2] = 1;
        for (int i = 3; i <= n; i++) {
            array[i] = array[i - 1] + array[i - 2];
        }
        return array[n];
 }

　　空间复杂度：额外定义了一个数组;空间复杂度依然是0(n)，但是没有递归产生的空间。

　　 时间复杂度：时间复杂度是0(n)

　　方案4： 滚动数组降低空间复杂度;

　　 对于斐波拉契数列，只需要2个数组空间即可;

 public int fib(int n) {
        if(n <= 2) return 1;
        int[] array = new int[2];
        array[0] = array[1] = 1;
        for (int i = 3; i <= n ; i++) {
            array[(i - 1) & 1] = array[(i - 1)  & 1] + array[(i - 2) & 1];
        }
        return array[( n - 1)  & 1];
    }

　　空间复杂度：额外定义了一个数组;但是长度只有2，所以空间复杂度0(1);

　　 时间复杂度：时间复杂度是0(n)

　　方案5：定义2个变量代替数组

 public int fab5(int n) {
        if(n <= 2) return 1;
        int n1 = 1;
        int n2 = 1;
        for (int i=3;i<=n;i++) {
            n2 = n1 + n2;
            n1 = n2 - n1;
        }
        return n2;
 }

　　空间复杂度：不需要额外定义数组，只定义2个变量即可，所以空间复杂度0(1);

　　时间复杂度：时间复杂度是0(n)

　　方案6：使用线性方程;

　　方案7:利用尾递归实现，java可以对尾递归的栈空间优化

    public int fab7(int n) {
       return fab7(n,1,1);
    }

    public int fab7(int n, int n1,int n2) {
        if(n <= 2) {
            return n2;
        }
        return fab7(n - 1,n2,n1+n2);
    }

　　空间复杂度：递归的深度为0(n)，但是由于是尾递归，优化后的空间复杂度是0(1)

　　时间复杂度：时间复杂度是0(n)